„eins zwei drei vier fünf sechs sieben... Eine Geschichte des Zählens und der Zähler“
Wegra-Verlagsgesellschaft in Stuttgart, zum 125jährigen Bestehen der Zählerfabrik J. Hengstler KG in Aldingen
Text Claus D. Grupp
Am Anfang war die Zahl
Kurioses und Mysteriöses aus der Welt der Zahlen
Was gezählt ist, steht fest. Über alles andere kann man sich streiten. Zahlen beweisen, schrieb Benzenberg vor hundertfünfzig Jahren. Typisch: Er war Physiker. Solche Leute und verwandte Berufe neigen dazu, die Welt in Zählbares, Wägbares, Messbares zu zerlegen. Manche von ihnen gelangen schließlich gar zu der Überzeugung, alles, was sich nicht in Zahlen fassen lasse, sei schlechthin unfasslich, wenn nicht gar dubios und eine arge Täuschung der Sinne.
So dachte vermutlich auch jener Geschichtsschreiber, der den historischen Augenblick festhalten sollte, als der große Inka 1532 den spanischen Gesandten und Abenteurer Hernando de Soto empfing. Die Inkas nämlich dachten in Zahlen, ja sie schrieben gar in einer Art Zahlschrift, vermittels Knoten, Doppelknoten, und zwei- bis neunfachen Schlingknoten auf ihren Quipus. Diese Knotenschnüre knüpften beispielsweise die Camayocs, die in jedem Dorf saßen und damit die amtlichen Unterlagen für die Berechnung von Abgaben und Steuern an die Regierung in Cuzco lieferten. Aber nicht nur Zahlen und Daten, auch Verträge, Gesetze und ihre ganze Geschichte schrieben die Inkas in Zählknoten auf Schnüre. So sollten am Hofe in Cuzco auch zwei Ayutas, zwei Schreiber, die Botschaft des spanischen Gesandten und die Antwort des Inka für die Nachwelt knüpfen. In der Nähe eines dieser Schreiber stand Garcilasso de la Vega, Sohn einer reizenden Inkaprinzessin und eines Spaniers; er kannte die Quipu-„Schrift“ und war zugleich des Spanischen mächtig, und er kritisierte die Knüpferei des Ayuta: „Seine Übersetzung war nicht gut und nicht schriftgemäß; aber nicht absichtlich, denn er verstand nicht den Sinn dessen, was er zu übersetzen hatte. Statt ,dreieiniger und ein Gott' las er ,drei Götter und einer sind vier', indem er die Zahlen zusammenzählte, um so die Sache für sich verständlich zu machen.“ Für einen, der in Zahlen denkt, sind eben auch Götter in Zahlen zerlegbar.
Nun lassen sich allerdings sogar scheinbar vage, unbestimmbare Aussagen, wenn man nur gründlich genug ist, mit Zahlen belegen. Die Farbe eines Lindenblattes in der Herbstsonne zum Beispiel; sie mag auf einen Maler augenscheinlich anders wirken als auf einen Buchhalter – sie ist also relativ, aber nur scheinbar. Wer es will, kann die Farbe physikalisch zerlegen und sie in Wellenlängen und deren Mischungsverhältnis mathematisch exakt bestimmen. Womöglich wird ein Zahlenbegeisterter sich an den spektralanalysierten Daten einer Farbe sogar mehr begeistern als an der Farbe selber. Jedenfalls ist eine so vielschichtige Sache wie die Farbe eines Herbstblattes, die zehn Dichter zehnmal verschieden beschreiben, zehn Maler zehnmal verschieden malen würden, unumstößlich messbar. Ja, vermutlich lässt sich selbst die faszinierende Ausstrahlung einer schönen Frau auf irgendeine Weise messen, etwa in erhöhten Pulszahlen des angestrahlten Mannes, wenn nicht gar in Kalorien auf Grund erhöhter Wärmeproduktion des Körpers. Aber welcher Mann möchte schon bei der Betrachtung einer Frau wissen, dass seine zusätzlich erzeugte Kalorienmenge zwölf Gramm Wasser oder wieviel auch immer zum Sieden bringen könnte! Mit anderen Worten: Fast alles lässt sich in Zahlen ausdrücken, aber man legt nicht in allen Fällen Wert darauf.
Und es bleiben vielleicht auch ein paar Aussagen, die sich absolut nicht in Zahlen fassen lassen, und gerade sie geben dieser zerlegbaren, untersuchbaren, messbaren Welt den Hauch von neugierweckender Ungewissheit, von träumerischer Romantik, von unfassbarer Unendlichkeit – wenn sie auch dem Zahlenmenschen oder dem logistischen Philosophen ein Greuel sein mögen. Das Unwägbare ist eben der Rest Göttlichkeit in einer entzauberten Welt.
Solange aber die Farben eines Herbstwaldes nicht nur als physikalische Messgrößen interessieren, solange ein Akkord noch wie Musik in den Ohren klingt und nicht nur als Wellengemisch im Oszillographen erscheint – solange dürfen Schlagertexter noch darauf hoffen, verstan-den zu werden, wenn sie behaupten: Was wirklich zählt auf dieser Welt, bekommst du nicht für Geld. Wobei seltsam ist, dass gerade das zählen soll, was nicht gezählt werden kann, nicht in Zahlen zu fassen ist. Die Sprache erlaubt sich da schon amüsante Eskapaden. Sprache und Zahlen haben ohnehin recht eigenartige, oft dunkle Verbindungen. Wenn zum Beispiel die Oma ihren Enkeln ein Märchen erzählt, so hat das auf uralte Weise durchaus etwas mit Zählen zu tun, wenigstens etymologisch gesehen.
Unser Wort Zahl leitet sich nämlich vom urgermanischen „talo“ ab; so hieß der Einschnitt auf dem Kerbholz, den man zählen konnte. Nun machten aber die alten Germanen ihre gesamte Buchführung mit dem Schnitzmesser, nicht weil es sich auf dem Bärenfell leichter schneiden als schreiben ließ, sondern weil kaum jemand überhaupt schreiben konnte. Wenn nun ein Verwalter von Haus und Hof Bericht erstattete über Viehbestand oder Vorräte, so zählte und erzählte er, was er auf dem Kerbholz hatte. Im Laufe der Zeit bekam „tal“ deshalb die Bedeutung von Zahl und von Rede. Im Englischen heißt Erzählung ja heute noch „tale“; ein „teller“ aber ist nicht nur ein Erzähler, sondern auch der Stimmenzähler im Parlament und der Kassierer in der Bank, der das Geld zählt. Hier hat sich in der Sprache buchstäblich das Mittelalter in die Gegenwart hinübergerettet. Auch bei uns hatte noch im Mittelhochdeutschen „zal“ sowohl die Bedeutung von Zahl, Menge als auch von Rede, Erzählung. Man kann also, sprachgeschichtlich gesehen, behaupten: Im Anfang war die Zahl – und damit Doktor Faustens Qualen bei der Übersetzung des Johannes-Evangeliums auf andere Art lösen, als Goethe es tat: „Geschrieben steht: ,Im Anfang war das Wort!' Hier stock ich schon! Wer hilft mir weiter fort?... Mir hilft der Geist! Auf einmal seh ich Rat und schreibe getrost: ,Im Anfang war die Tat!'“ Tatsächlich war's die Zahl; sie kam wenigstens in der Sprache vor der Rede, dem Wort.
Wer aber suchet, der findet noch mehr und engere Verbindungen zwischen Zahl und Sprache. In Hunderten von Worten stecken Zahlen, mitunter sofort erkennbar (wie in Erstgeburt, zweierlei, Dreirad, Vierkant, Fünfeck), manchmal etwas versteckter (wie in Prinz, Primel, Zwiebel, Zwieback, Drell, Quartier), gelegentlich aber auch kaum noch zu finden, vor allem, wenn es sich um fremdsprachliche Zahlwörter handelt. Wer vermutet schon im Geschwader, im Punsch oder im Lack Zahlen als Wurzel! Aber fangen wir bei der Zwei an; sie ist versteckt im Zwirn, im Zweig, im Geweih, im Zwicken und sogar im Zuber: Das war im Althochdeutschen ein zwibar, ein zweihenkliges Gefäß im Gegensatz zum einbar, dem Eimer. Drei findet man im Drillich oder Drell, dem dreifädigen Leinengewebe, und im Testament: Der Zeuge hieß lateinisch testis, und das war entstanden aus tri-stis: als dritter danebenstehend. Wo hat sich die Vier versteckt? Im Geschwader; es stammt vom italienischen squadrone, worin das lateinische quadra, das Viereck, steckt. Ein Geschwader war im Mittelalter eine im Viereck geordnete Reitertruppe.
Einen weniger kriegerischen Hintergrund hat sich die Fünf ausgesucht – sie schwimmt im Punsch. Dieses ursprünglich südostasiatische Getränk wird aus fünf Zutaten gemixt: Arrak, Zucker, Zitronensaft, Gewürz und Wasser. Fünf heißt aber hindostanisch „pantsch“, und das haben indienreisende und trinkfreudige Engländer anglisiert und als „punch“ in ihre Sprache übernommen, woraus dann unser Punsch wurde. Auch die Sechs ist friedlicher untergebracht, in der Siesta nämlich, der – nach alter Zwölfstundenzählung – sechsten Stunde des Tages, dem Mittag also, und außerdem im Samt, dem sechsfädigen Seidenstoff, den die Griechen hexämiton nannten, wovon der Zahn der Zeit das he- abbiss, so dass ein -xamiton übrigblieb, woraus leicht unser Samt werden konnte.
Wollte man, könnte man noch seitenweise zahlenträchtige Wörter aufzählen; lassen wir's aber bei zwei, drei historisch interessanten Beispielen für höhere Zahlen bewenden. Im Jahre 1435, zwei Jahre nach seiner Krönung zum deutschen Kaiser und zwei Jahre vor seinem Tode, erließ König Sigismund von Ungarn ein Gesetz, wonach jeder ungarische Grundbesitzer für je zwanzig Leibeigene einen bewaffneten, berittenen Soldaten stellen musste. Nun heißt aber zwanzig im Ungarischen „husz“ – die Reiter waren die Husaren.
Anno 1374 mussten erstmals Schiffe, die Venedig anliefen, zur Beobachtung auf Pest eine Zeit lang im Hafen liegen, ehe Besatzung und Reisende an Land durften; ab 1400 erhielten dann auch in anderen italienischen Häfen pestverdächtige Seereisende eine Ausgangssperre von „quaranta giorni“, von vierzig Tagen – so entstand das Wort Quarantäne. Und ein letztes Exempel: In unserem Wort Lack steckt das indische Zahlwort Iakscha, hunderttausend, und das kam so: In Indien gibt es eine Schildlaus, die in unzählbaren Massen vorkommt; da „lakscha“ nicht nur Zahlwort für 100 000 ist, sondern übertragen auch „Unzahl, Riesenmenge“ bedeutet, wurde die Schildlaus Lakscha genannt; sie sticht in die Blätter einer bestimmten Pflanze, die daraufhin eine harzige Flüssigkeit absondert, die das Blatt wie mit glänzendem Lack überzieht – der Rest versteht sich von selbst.
Man sieht: Zahl und Zählen führen, wenn auch auf Umwegen, mitunter zu unerwarteten Ergebnissen. Und umgekehrt: Erhoffte, zu bestimmter Zeit erwartete Ereignisse werden oft durch Zählen oder Abzählen eingeleitet, bisweilen wird ihre Ankunft sogar durch Zählen wie mit einer Zauberformel herbeibeschworen: der Schlaf am Abend durch das Schäfchenzählen, der Raketenstart durch den Count down, der Knock out durch das Sekundenzählen, der Sucher beim Versteckspiel durch den Abzählreim. Man zählt dabei laut oder leise, gelassen oder voller Ungeduld, mündlich oder mechanisch, exakt oder nach Gefühl. Dass man das Abzählen aber auch auf vitaminreiche Weise bewerkstelligen kann, hat Adalbert Stifter gezeigt, als er eine Art Liebes-Count down mit Obst erfand: Er legte je einen Apfel beiseite für jeden Tag bis zum Wiedersehen mit seiner Braut, und täglich aß er einen Apfel auf. Der Braut schrieb er: „Noch immer liegen 14 Äpfel da; aber doch nur mehr 14. Als ich den vorvorigen Brief schrieb, waren es 21; das ist doch nun ein Trost, morgen sind es nur mehr 13! Und endlich wird es doch nur mehr einer sein, und wenn ich diesen gegessen habe, erhebe ich ein Jauchzen.“ So poetisch vermochte ein Dichter im Biedermeier zu zählen.
Bildkräftig können auch die Inder eine Zahl benennen. Sie kennen neben ihren Zahlwörtern unzählige Umschreibungen für Zahlen, allein etwa dreihundert für die Zahlen eins und zwei. So können beispielsweise alle Dinge, die paarweise vorkommen, für das Zahlwort „zwei“ stehen, etwa Augen oder Arme. Die nüchterne Zahl 1021 kann ein Inder auch so ausdrücken: saschi-paksa-kha-aka, was wörtlich heißt: Mond-Flügel-Loch-eins, in Zahlen also: 1021 (die Inder lesen den Stellenwert nämlich genau umgekehrt wie wir, die Einer stehen also ganz links). Die Umschreibung für die Null erinnert daran, dass diese Ziffer tatsächlich einem Loch (Nichts mit etwas drumrum) ähnelt. Und wem das Bild nicht schön genug erscheint: Die Inder können schließlich mit der Null machen, was sie wollen, denn sie ist ihre ureigene Erfindung – und eine der bedeutendsten für das Zählen überhaupt.
Die alten Griechen, die alten Römer, sie kannten ja die Null noch nicht, die so segensreich sein kann, wenn sie nur an der richtigen Stelle steht. Und deshalb kannten sie auch nicht den Stellenwert der Ziffern und mussten für jede höhere Zählstufe gleich ein neues Zeichen erfinden und konnten mit ihren Zahlenungetümen aus Buchstaben nur so schwer rechnen wie ein ABC-Schütze heute mit höheren Potenzen. Die handelstüchtigen Araber aber, in deren Händen anfangs Handel und Geldwechsel lagen, da die Christen bis ins Mittelalter wegen des kanonischen Zinsverbotes keine lukrativen Geldgeschäfte betreiben durften, diese rechnenden und berechnenden Araber also haben etwa im 9. Jahrhundert die kaufmännische Bedeutung der Stellenwertschreibung erkannt und das indische Dezimalsystem nach Vorderasien und Europa buchstäblich eingeschleppt – die Europäer betrachteten nämlich das neumodische Ziffernsystem lange mit äußerstem Misstrauen. Noch gegen Ende des 13. Jahrhunderts erließ Florenz Gesetze, die den Gebrauch der Dezimalziffern verboten, und Florenz war seinerzeit als Stadt mit einer der ersten Banken Europas keineswegs rückständig.
Übrigens sträubten sich nicht nur die Italiener, sondern auch andere Völker, vor allem die Deut-schen, gegen die Ablösung der römischen Zahlschrift, die man hierzulande nachgerade schon für „die gewönlich teutsch zal“ hielt, wie der Rechenmeister Köbel Anno 1514 schrieb. Freilich, man war gegen die indisch-arabischen Ziffern nicht allein deshalb, weil sie fremd waren. Die Bankiers und Kaufleute etwa fürchteten Fälschungen auf Schuldscheinen und Zahlungsanweisungen, da aus einer indischen Null leicht eine Sechs oder Acht oder Neun gemacht werden konnte. Allerdings: Fälschungssicher waren die römischen Buchstabenzahlen auch nicht gewesen, und dass Fälschungen seinerzeit nicht gerade selten waren, davon zeugt die bis heute unvergessene Lebendigkeit des Sprichworts: ein X für ein U vormachen, also aus einer Fünf eine Zehn machen (V und U waren früher identisch).
Der Übergang von der alten zur neuen Schreibweise, dem Volke verdeutlicht auf Tafeln mit der „verglychung tüdtscher und ciferzal“, dauerte hier kürzere, dort längere Zeit. Rasch von Begriff waren offensichtlich die Bayern. Da starben gegen Ende des 15. Jahrhunderts die alten Rittersleut Ludwig und Hans von Paulsdorf. Auf ihrem Grabstein (er steht heute im Bayerischen Natio-nalmuseum in München) ist das Todesjahr Ludwigs noch in römischer Schreibweise eingemeißelt; er starb „Anno dm mcccclxxxij am pfinztag vor vith“, also 1482 am Donnerstag vor Veit. Ritter Hans starb nur zwölf Jahre später, aber sein Todesjahr ist bereits in Ziffern eingehauen; er starb „darnach im . 94. am freitag vor liechtmessen“.
Die Kaufleute waren's vor allem, die den indischen Ziffern zum Sieg über die römischen Zahlzeichen verhalfen, denn: Mit der Zahlenschreibweise nach Stellenwert konnte man endlich bequem rechnen, konnte man schlicht auf dem Papier addieren und subtrahieren, ohne Hilfe der Finger oder des Abakus. Im ganzen Mittelalter hatten die Leute noch an den Fingern gerechnet, sogar multipliziert, wenn es auch nur wenige waren, die es überhaupt konnten. Bruder Berthold von Regensburg, ein populärer Prediger im 13. Jahrhundert, hatte einst vom Zählen und Rechnen an den Fingern geschrieben: „Des kunnet ir ungelernten Liute niht, wan es ist der gelerten vil, di es niht kunnent.“
Die es aber kunnten, die machten es so: Sollten sie etwa 7 mal 9 rechnen, so bogen sie je einen Finger einer Hand für jede über 5 hinausgehende Zahl eines Faktors, an der einen Hand also zwei, an der anderen vier Finger. Die Summe der gebeugten Finger ergab die Zehner des Produkts: 2+ 4= 6, also 60. Danach vervielfachten sie die Zahlen der nicht gebeugten Finger beider Hände miteinander, das ergab die Einer, also 3 mal 1; das Ergebnis war demnach 63 – und siehe da, es stimmt. Die Fingerrechnerei hatte nur ein paar Haken: Wer sich einen Finger abgehackt hatte, kam immer aufs falsche Ergebnis; außerdem konnte man nur Faktoren zwischen 5 und 10, auf etwas andere als die beschriebene Weise auch bis 15 miteinander multiplizieren, und schließlich musste man das kleine Einmaleins bis einschließlich 5 mal 5 entweder im Kopfe haben oder von Tabellen ablesen können.
Die alten Ägypter hatten da zwar auf primitivere Weise multipliziert, aber sie konnten mit ihrem Verfahren wenigstens auch höhere Zahlen miteinander vervielfachen und brauchten keinerlei andere Voraussetzungen als die, mehrere Zahlen zusammenzählen zu können. Sie waren nämlich auf einen einfachen, aber wirkungsvollen Trick gekommen: Sie hatten bemerkt, dass man jede Multiplikation in zwei Vervielfachungsstufen zerlegen kann, die sehr einfach sind: in Verdoppelungen und Verzehnfachungen. Musste ein alter Ägypter beispielsweise 27 mal 63 rechnen, so schrieb er scheinbar wahllos die doppelten und zehnfachen Werte des einen Faktors untereinander und zählte dann die passenden Zahlen zusammen:
1 X 63
10 x 630
20 X 1260
2 X 126
4 X 252
Zählte er nun die Einer-, Zweier-, Vierer- und Zwanzigerwerte (1 + 2+ 4 +20=27) zusammen, so hatte er das Ergebnis: 1701. Etwas umständlich vielleicht, aber damals hatte ja man noch etwas, was wir heute kaum noch kennen: Zeit.
Wie das Fingerrechnen bis vor kurzer Zeit noch in der rumänischen Walachei und der französischen Auvergne lebendig war, so hat sich eine eigenartige Variante der uralten ägyptischen Addier-statt-multiplizier-Methode in Russland lange erhalten. Dort rechnete man auf dem Lande noch bis zum ersten Weltkrieg auf eine verblüffende Weise; warum sie stets funktioniert, das zu beweisen fällt selbst einem geübten Mathematiker nicht ganz leicht. Hatte etwa ein russischer Kulak Äcker, die zusammen 37 Werst lang und 27 Werst breit waren, und wollte er wissen, welche Fläche da sein eigen war, so musste er Länge mit Breite multiplizieren, und das bewerkstelligte er so: Er halbierte den einen Faktor so oft, bis er auf die Eins kam; dabei schrieb er nur ganze Zahlen auf, entstehende Halbe ignorierte er einfach. Die halbierten Zahlen schrieb er nun untereinander, daneben trug er in eine zweite Spalte die Zahlen ein, die entstanden, wenn er den zweiten Faktor so oft verdoppelte, wie er den ersten halbiert hatte. Das ganze sah dann so aus:
37 27
18 54
9 108
4 216
2 432
1 864
Und nun kam der Trick: Er strich in der Halbierungsspalte alle geraden Zahlen und auch die entsprechenden in der zweiten Spalte (hier: unterstrichen) und zählte danach die übriggebliebenen Verdoppelungszahlen zusammen – das Ergebnis stimmte immer:
37 27
18 54
9 108
4 216
2 432
1 864
999
Das Verblüffende jedoch: Geübte Mathematiker, Programmierer zum Beispiel, benützen heute noch diese Halbierungsmethode; allerdings nicht, um zu multiplizieren (dazu nehmen sie wie ein Buchhalter-Lehrling die Rechenmaschine), sondern um rasch den binären Ausdruck einer Dezimalzahl zu finden. Das binäre Zahlensystem – das einzige, das ein Computer versteht – geht bekanntlich auf Leibniz zurück und ähnelt der Zählweise mancher Südseestämme, die nicht bis drei zählen können; drei ist bei ihnen zwei-eins, vier ist zwei-zwei und so weiter. In einem Südsee-Dialekt klingt das Abzählen beispielsweise so: urapun / okasa / okasa-urapun / okasa-okasa / okasa-okasa-urapun / okasa-okasa-okasa / okasa-okasa-okasa-urapun – und so weiter. Man versteht nun, warum ein alter Südsee-Insulaner in Schwierigkeiten gerät, wenn er nach seinem Alter gefragt wird. Und man stelle sich vor, wie es am Ende klänge, wenn ein in die Südsee verschlagener preußischer Feldwebel eine Kompanie Eingeborener in Reih und Glied aufstellen und abzählen ließe: Eins, Zwo, Drei, Vier, natürlich auf Insulanerisch.
Ähnlich wie die Südseeler baute Leibniz sein binäres Zahlensystem nur aus zwei Ziffern auf, aus Null und Eins. Null ist 0, Eins ist 1, Zwei ist 10, Drei 11, Vier 100, Fünf 101, Sechs 110, Sieben 111, Acht 1000, Neun 1001, Zehn 10010, und so weiter ad libitum et infinitum. Es versteht sich von selbst, dass ein Mathematiker nicht die ganze unendliche Zahlenreihe dezimal und binär im Kopf haben kann, er schaut also in Tabellen nach, wenn er wissen will, wie die Zahl 312 im binären (oder Dual-)System heißt. Hat er aber sein Schaunach mal verlegt, so hilft er sich auf wie der russische Großbauer: Er halbiert seine Dezimalzahl so oft, bis Eins herauskommt und lässt dabei entstandene Halbe ebenfalls fallen; nun schreibt er neben die geraden Zahlen eine Null, neben die ungeraden eine Eins, und schon hat er die Binärzahl, zum Beispiel von 37:
37 1
18 0
9 1
4 0
2 0
1 1
Der binäre Ausdruck für die Dezimalzahl 37 ist also 101001. So einfach ist das – wenn man's weiß.
Im übrigen weiß man, dass ein Elektronenrechner zwar rasend schnell, im Grunde aber auf recht einfache Weise rechnet; er kann ja schließlich auch nur zwei Ziffern (oder genauer gesagt: nur den Unterschied zwischen Strom und Nicht-Strom) erkennen. Quadratwurzeln beispielsweise zieht er nach einem Verfahren, das dem der Zigeuner ähnelt. Kommt ein Czigan einmal in die Verlegenheit, außer essbaren auch mathematische Wurzeln ziehen zu müssen, so legt er zunächst seine Geige beiseite und sodann sich ins Zeug, wobei er ein verblüffend einfaches Verfahren anwendet: Er zieht von der Wurzelzahl nacheinander die aufsteigenden ungeraden Zahlen 1, 3, 5 und so weiter ab, bis er auf Null (oder einen Rest) stößt. Dabei merkt er sich die Zahl der Rechenschritte, denn sie ist das Ergebnis. Soll er zum Beispiel die Wurzel aus 36 ziehen, so beginnt er zu rechnen:
36-1 = 35; 35-3 = 32; 32-5 = 27;
1. 2. 3.
27-7=20; 20-9=11; 11-11= 0
4. 5. 6.
Sechs Rechenschritte brauchte er, also ist das Ergebnis 6. Stimmt. Exakte Ergebnisse lassen sich auf diese Weise freilich nur erzielen, wenn man die Wurzel gerade aus einer Quadratzahl ziehen muss, sonst geht die Abzieherei nicht mit Null aus; es bleibt dann ein Rest, und man muss die Kommastellen des Ergebnisses schätzen. Aber so arg genau nimmt's der Zigeuner vielleicht auch nicht, wenn es ums Wurzelziehen geht.
Die Zahl 37 übrigens, die wir weiter vorne auf russische Art mit 27 multiplizierten, ist eine der vielen Wunderzahlen, die von Mathematikern und Zahlenmystikern mit Fleiß gesucht werden. Multipliziert man sie nämlich mit Zahlen, die um jeweils 3 anwachsen, so erhält man, wenn man mit der Drei anfängt, ganz überraschende Ergebnisse:
3X37=111; 6 x 37=222; 9 X 37=333;
12 x 37= 444 und so weiter bis 27 x 37 = 999.
Ähnliche, nur ins Höhere transponierte Produkte bekommt man mit der Zahl 3367. Multipliziert man sie mit 33, so erhält man 111 111; mit 66 malgenommen ergibt sie 222222, mit 99 findet man 333 333 und so weiter, bis man bei 297 schließlich 999 999 bekommt.
Eine andere Wunderzahl entdeckte im Jahre 1936 der Professor Zervos in Athen: 142857. Auf den ersten Blick sieht sie ganz normal und harmlos aus; multipliziert man sie aber mit 2, 3, 4, 5 und 6, so enthalten auch die Ergebnisse die Ziffern 142 857 in gleicher, nur zyklisch fortgesetzter Reihenfolge (so dass auf die 7 wieder die 1 folgt, dann 4, 2, 8 und so weiter):
2 x 142857 = 285714
3 x 142857 = 428 571
4 x 142857 = 571 428
5 x 142857 = 714 285
6 x 142857 = 857 142
und schließlich zur Krönung: 7 x 142 857 = 999 999. Man kennt noch eine ganze Reihe solch wunderlicher Zahlen; zu ihnen kann man auch die vollkommenen Zahlen zählen, bei denen die Summe ihrer Teiler (einschließlich Eins) wiederum die Zahl selbst ergibt. Die erste vollkommene Zahl ist die Sechs, deren Teiler 1, 2 und 3 zusammen wieder 6 ergeben; als nächste ist die 28 vollkommen, unter den folgenden 30 Millionen Zahlen aber findet man nur noch zwei weitere vollkommene, nämlich 496 und 8128.
Sechserzahlen (wie 6, 12, 60 und so weiter) findet man wegen der „Vollkommenheit“ ihrer Grundzahl oft wieder, vor allem in sagenhaften und mythischen Darstellungen. Romulus, dem Gründer Roms, erschienen 12 Geier als Zeichen, und die Urbs Romana sollte 1200 Jahre dauern (eine Prophezeiung, die ihrer Erfüllung immerhin näher kam als jene spätere eines Tausendjähri-gen Reiches!). Bei Homer gebieten Ajax und Odysseus je über 12 Schiffe mit je 120 Mann Besatzung, und Eumäos, der göttliche Sauhirt, lässt seine 360 Eber weiden. Menelaos war Herr über 60 Schiffe; 12 ionische Städte schlossen sich zu einem Bund zusammen, und ein griechisches Schiff hatte 120 Böoter als Besatzung. Die 12 Stämme Israels und die 12 Apostel gehören ebenso in diese Reihe wie die geheimnisvollen Zahlen aus der Apokalypse, 666 und 144000. So heißt es in der Offenbarung Johannis, Kapitel 7, Vers 4: „Und ich hörete die Zahl derer, die versiegelt wurden, hundert und vier und vierzig tausend.“ Und in Kapitel 14, Vers 1: „Und ich sah das Lamm stehen auf dem Berg Zion und mit ihm hundert und vier und vierzig tausend.“ Auch darin steckt die vollkommene Sechs, denn 144 000 ist 103 mal 122. Viel rätselhafter aber ist der Vers 18 im 13. Kapitel: „Wer Verstand hat, der überlege die Zahl des Tieres, denn es ist eines Menschen Zahl, und seine Zahl ist sechs hundert und sechs und sechzig.“ Ungezählte Wissenschaftler und Laien haben versucht, diese Zahl zu entschlüsseln und damit zu beweisen, dass sie Verstand hätten. Eine unter vielen Lösungen: Es ist eine Verschlüsselung für „Kaiser Nero“. Schreibt man nämlich in der sonst griechisch verfassten Offenbarung den Namen Kaiser Neros hebräisch, so sieht das (in lateinische Buchstaben übersetzt) etwa so aus: nrwn qsr (die hebräische Schrift kennt ja keine Vokale); diese Buchstaben haben im Hebräischen aber den Zahlenwert:
50+200+6+50 + 100+60+200 = 666.
Nach einer Deutung aus jüngster Zeit ergibt auch der Name Adolf Hitler, in griechischen Buchstaben und deren Zahlenwert übersetzt, die Summe 666. Man kennt noch viele Beispiele für Isopsephie, wie man diese Spielerei mit Buchstaben und Zahlen nennt. So findet man am Ende griechischer Gebete oft zwei Buchstaben, die die Zahl 99 bedeuten (koppa theta, wobei koppa ein dem Q ähnlicher semitischer Buchstabe war). Die Lösung des isopsephischen Rätsels heißt: Amen, denn die Summe der Zahlenwerte dieser Buchstaben (die Griechen kannten ja keine Ziffern!) ergab 99: Alpha (1) + my (40) + eta (8) + ny (50).
Viel verbreiteter in Religion, Magie und Mystik als die Sechs sind jedoch die Drei und die Sieben. Die Drei war die erste „unerreichbare“ Zahl des Menschen, der in früher Stufe nur bis Zwei zählen konnte, nur das Ich und das Du kannte und darüber hinaus nur ein Viel. Was über zwei hinausging, war also viel und konnte unendlich sein, oder wenigstens unvorstellbar, denn eine „Vorstellung“ des Unendlichen war dem frühen Menschen nicht möglich. Die Drei war also das Sinnbild einer übersinnlichen, übernatürlichen Eins, oder anders gesagt: Drei war eine Vielheit dem Menschen, aber eine Einheit dem Göttlichen. Oder philosophisch ausgedrückt: Die Eins als indifferente These braucht die Zwei als Antithese, als Gegensatz, und beide verbindet die Drei als Synthese, als die höhere Einheit.
Nicht nur die christliche Religion, auch der Hinduismus kennt die Dreieinigkeit und nennt sie Trimurti: „Er, welcher Wischnu, ist auch Schiwa, und Er, welcher Schiwa, ist auch Brahma, ein Wesen, aber drei Götter.“ Wischnu ist die Erhaltung, Schiwa die Zerstörung und Brahma die Schöpfung. Auch die alten Ägypter hatten, bei aller Vielfalt ihrer Götter und trotz gelegentlicher monotheistischer Anwandlungen (Ra in Heliopolis), am häufigsten drei Götter anzubeten, wie immer sie auch geheißen haben mögen: Osiris-Isis-Horus, Ptah-Socharis-Osiris, Ptah-Sechmet-Imhotep, Amon-Mut-Khons. In der Regel handelte es sich um einen Obergott, seine Frau und einen Gott-Sohn.
Die griechische Mythologie kannte die drei Moiren, die drei Schicksalsgöttinnen Klotho (die den Lebensfaden spinnt), Lachesis (die ihn zuteilt) und Atropos (die ihn abschneidet). Ihnen entsprachen die drei Parzen der Römer und die drei Nornen der nordischen Mythologie: Urd (die Vergangenheit), Werdandi (die Gegenwart) und Skuld (die Zukunft). Drei Grazien kannten die Römer, entsprechend den drei Charitinnen der Griechen: Aglaia (Festesglanz), Euphrosyne (Frohsinn) und Thalia (blühendes Glück). Dreigestaltig war Hekate, die Zaubergöttin, dreifach die Fruchtbarkeit des persischen Sonnengottes Mithra. Dreimal umschritten die Germanen ihre Altäre, und als sie schließlich bekehrt waren, erkannten sie in der christlichen Dreieinigkeit ihre drei alten Götter: Odin, Thor und Freya. Drei Stufen führten zu den antiken Tempeln, Dreifüße schenkten die Griechen ihren Göttern zur Weihe. Einen Dreizack hatte Neptun, einen dreigeteilten Glücksstab Merkur, der Handelsgott. Dreieckig ist das Symbol des Gottesauges in der christlichen Vorstellung. Das Triumvirat, die Trigonometrie, die drei Zeiten, drei Geschlechter, drei Steigerungen in der Grammatik – immer und überall stößt man auf die Drei. Und da wir schon bei dieser Zahl sind: Immer wieder hört man die Scherzfrage, welches wohl die größte Zahl sei, die mit drei Ziffern zu schreiben ist. Natürlich: 9 hoch 9 hoch 9, also 999; 99 ergibt 387 420 489. Multipliziert man diese Zahl nun neunmal mit sich selbst, so ergibt sich eine Zahl, die selbst das Fassungsvermögen eines Computers sprengen würde: sie hat 369 693100 Stellen. Wollte man die Zahl aufschreiben und benötigte für je zwei Ziffern einen Zentimeter Platz, so hätte man am Schluss einen Papierstreifen von rund 1850 Kilometern Länge vollgeschrieben. Mathematische Tüftler kennen freilich eine noch größere Zahl mit drei Ziffern: 9!9!9!.
Was dem einen die Drei, ist dem andern die Sieben; sie hat schon lange vor unserer Zeitrechnung die religiösen Vorstellungen der Sumerer, der Inder und der Ägypter beeinflusst. Sieben Welten, sieben Flüsse und sieben böse Geister glaubte man im Zweistromland schon viertausend Jahre vor Christi Geburt zu kennen; sieben Himmel und sieben Höllen sahen die Inder, ihr Gott der Sonne sandte sieben Strahlen aus. Die erste Dynastie in Ägypten hatte sieben Götter, sieben aromatische Essenzen verwendete man zum Einbalsamieren der Leichen; sieben Planeten kannten die Babylonier und deshalb hat unsere Woche sieben Tage. Die Perser glaubten an sieben gute und sieben böse Geister, ihr Staatsrat musste aus sieben Männern bestehen. Sieben kluge Meister treten im Gilgamesch-Epos auf, sieben Weltwunder kannte die Antike. Apollo hatte nicht wie jedes Ding zwei, sondern sieben Seiten, am siebten Tag vor Neumond opferte man ihm. Sieben Berater hatten Agamemnon und Priamus, sieben Helden zogen vor das siebentorige Theben, Rom wurde auf sieben Hügeln erbaut, sieben Reliquien hütete der römische Staat, ein Geheimnis musste siebenmal versiegelt werden, sieben Testamentszeugen gab es nach römischem Recht und sieben Schöffen nach germanischem. Vor sieben Todsünden hat sich ein Christenmensch zu hüten, sieben Wochen soll er fasten, sieben Wochen nach Ostern feiert er Pfingsten. Siebenmal muss der Mekka-Pilger den Hadschar, den heiligen schwarzen Stein in der Kaaba umschreiten. Sieben Weise kannte man, sieben Säulen der Weisheit, sieben fette und sieben magere Jahre, den siebten Himmel, die sieben Locken Simsons, die sieben Zwerge, die sieben Schwaben, die Siebenmeilenstiefel, die sieben Häute der Zwiebel, die sieben Leben der Katze und so weiter und so fort; man könnte leicht sieben Seiten oder gar sieben Bücher damit füllen – man muss da schon etwas aussieben. Deshalb nur noch zwei letzte Beispiele für die Sieben: Im ältesten Rechenbuch, das wir kennen und das erhalten geblieben ist, dem des Ägypters Ahmes, der es um 1800 v. Chr. auf einen Papyrus schrieb, steht dieses Rätsel: Sieben Personen haben je sieben Katzen, jede Katze frisst sieben Mäuse, jede Maus frisst sieben Ähren Gerste, jede Gerstenähre hat sieben Maß Körner – wieviel Maß Getreide haben wir den Katzen zu danken? Nun, wir Heutigen haben's rasch raus: Es sind natürlich 7<sup>5</sup> oder 16 807 Maß Gerste; aber man erinnere sich, wie mühsam die Ägypter multiplizierten! Und das letzte Beispiel: Auf unseren Spielwürfeln ergänzen sich die Zahlen auf einander gegenüberliegenden Seiten stets zu 7; liegt zum Beispiel die Eins oben, dann ist die Sechs unten, der Vier liegt die Drei gegenüber, der Fünf die Zwei.
Die vermutete magische Wirkung von Zahlen konnte noch erhöht werden, indem man aufeinanderfolgende Zahlen in magischen Quadraten anordnete. Amulette mit solchen Zahlenquadraten trug man in China und Indien zum Schutz gegen allerlei Unbilden.
Das älteste erhaltene magische Quadrat ist dreigliedrig, besteht also aus drei waagrechten und drei senkrechten Reihen. Es ist in einer uralten chinesischen Handschrift gefunden worden, deren Alter man nicht mehr genau festlegen kann. Es ist nicht in Ziffern, sondern in Punkten geschrieben und zeigt diese Anordnung:
4 9 2
3 5 7
8 1 6
Berühmt ist das viergliedrige magische Quadrat auf dem Stich Melencolia I von Dürer; es enthält in der Mitte der untersten Reihe das Jahr, in dem der Stich entstand, 1514:
16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
Es ist das früher als Jupiter-Sigel bekannte Quadrat. Die Summen der Zahlen in den vier waag-rechten und den vier senkrechten Reihen ist immer 34, aber auch die Summe der Zahlen in den beiden Diagonalen; und ebenfalls 34 ergeben die jeweils vier Zahlen in den fünf Teilquadraten, die man aus dem Gesamtquadrat herausnehmen kann, zum Beispiel des Teilquadrats links oben:
16 3
5 10
oder in der Mitte:
10 11
6 7
Es gibt übrigens, wenn man von Drehungen und Spiegelungen einmal absieht, nur ein einziges magisches Quadrat mit drei Gliedern, aber bereits 880 viergliedrige. Eine für den Uneingeweihten verblüffende Sache (und damit eine eindrucksvolle Unterhaltung eines Gesellschaft): Man kann magische Quadrate mit ungerader Gliederzahl (fünf oder sieben Reihen zum Beispiel) blitzschnell selber herstellen, wobei man einem Zuschauer sogar noch die Wahl überlassen kann, mit welcher Zahl man beginnen oder welche Quersumme in den Waagrechten, Senkrechten und Diagonalen herauskommen soll. Das Verfahren dazu hat Emanuel Moschopoulos etwa um 1300 beschrieben. Er war ein Grieche, der in Konstantinopel lebte und der vermutlich als erster die magischen Quadrate aus Indien und China nach Europa brachte.
Man zeichne zunächst die leeren Kästchen eines magischen Quadrates mit ungerader Gliederzahl auf, also mit fünf oder sieben oder neun waagrechten und senkrechten Reihen. Zur rascheren Beschreibung nehmen wir hier als Beispiel nur ein Quadrat mit fünf Reihen, also mit 25 Feldern. Die erste Zahl (wir wollen mit der Eins beginnen) kommt in das Kästchen, das genau unter dem Schnittpunkt der beiden Diagonalen liegt; die folgenden Zahlen werden nun immer in der Richtung schräg rechts nach unten eingetragen, also parallel zur Diagonalen von links oben nach rechts unten. Gelangt man an den Rand des Quadrats, so schreibt man auf der gegenüberliegenden Seite weiter, so als wäre sie zyklisch dort angeschlossen, wo man eben aufhören musste. So sieht also der Anfang aus:
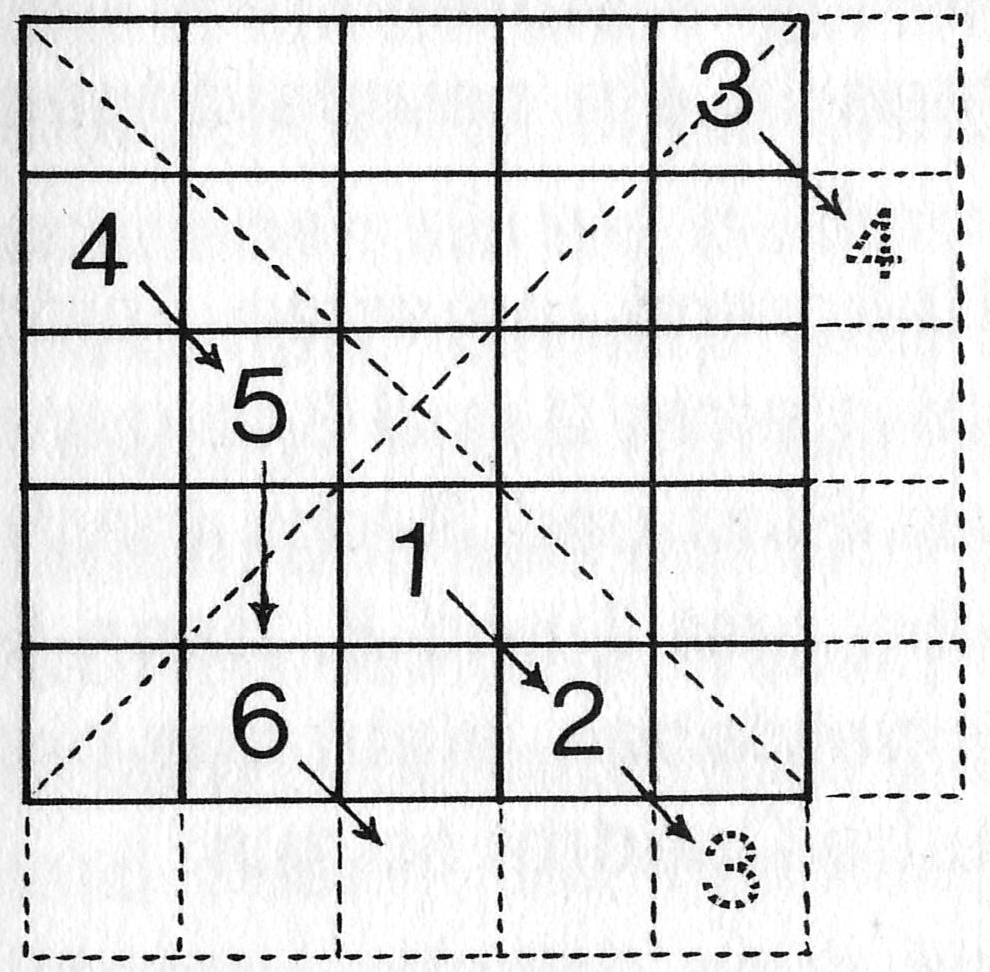
Mit der 2 kam man an den unteren Rand und trägt nun die 3 oben ein, als wäre diese Reihe unten angesetzt; die 3 stößt nun ihrerseits an den rechten Rand und man schreibt links weiter, als wäre das ganze Quadrat rechts angeschlossen. 4 und 5 können nun nacheinander in die folgenden Kästchen gesetzt werden. Mit der 5 stößt man aber an ein bereits (hier mit der Eins) besetztes Feld; in diesem Falle trägt man die nächste Zahl in das zwei Reihen darunterliegende Kästchen ein. Käme man damit übers Quadrat hinaus, müsste man sich nur wieder den oberen Teil unten angesetzt denken und dort weiterschreiben. Die folgenden Eintragungen sehen also so aus:
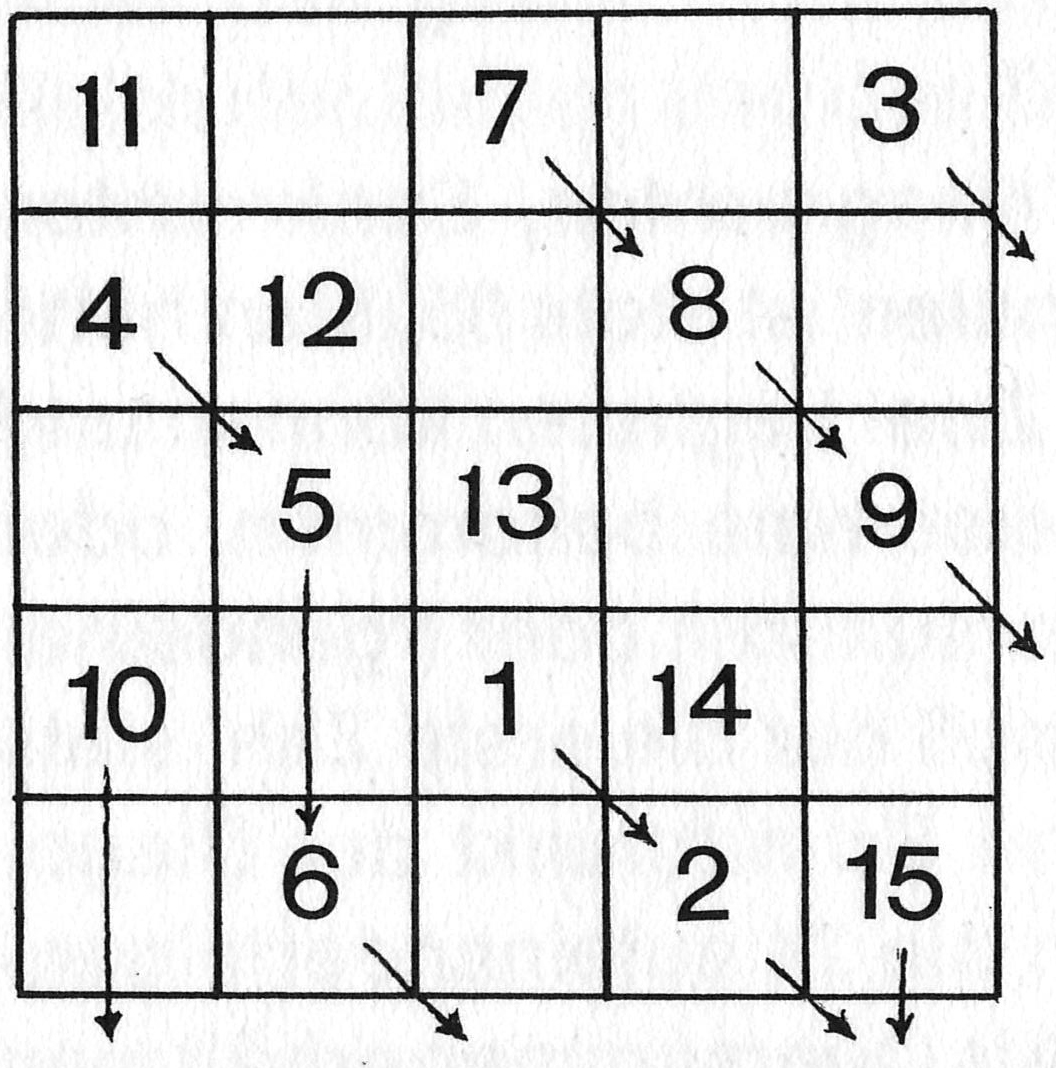
Mit der 15 gelangt man ins Endfeld der einen Diagonalen und fährt fort, als wäre ein folgendes Feld bereits besetzt, geht also in das zwei Reihen „tiefer“ liegende Kästchen, also in die zweite Reihe von oben. Nun (und wenn man den Bogen erst mal raus hat) ist es einfach, das ganze Quadrat zu füllen:
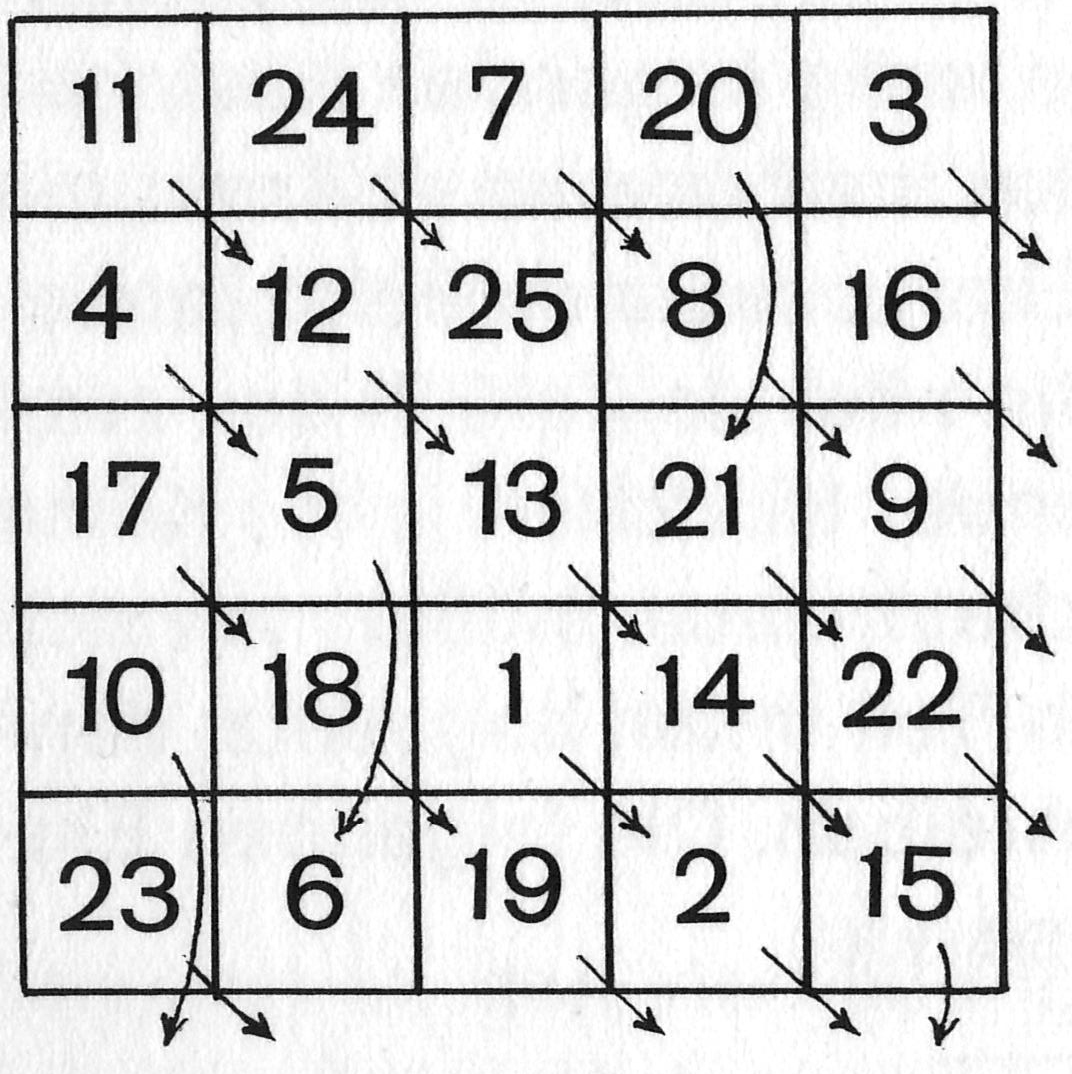
Die Quersumme der Waagrechten, Senkrechten und der beiden Diagonalen ist stets 65. Man hätte natürlich auch mit der Zwei beginnen können und hätte dann 70 als Quersumme bekommen, oder mit der Drei (75 als Quersumme) oder irgendeiner beliebigen Zahl. Man muss nur die erste Zahl stets in das Kästchen unterm Schnittpunkt der Diagonalen setzen und dann die 24 aufeinanderfolgenden Zahlen eintragen. Als Quersummen erhält man stets Fünfer- oder Zehnerzahlen, und zwar wird die Quersumme immer um 5 höher, wenn man die Anfangszahl um 1 erhöht. Wird also beispielsweise die Quersumme 100 verlangt, so muss man mit der 8 beginnen.
Übrigens glauben manche Deuter auch in Goethes Faust die Anleitung zur Herstellung eines magischen Quadrats gefunden zu haben, und zwar im berühmten Hexen-Einmaleins:
Aus Eins mach Zehn,
Und Zwei lass gehn,
Und Drei mach gleich,
So bist du reich.
Verlier die Vier!
Aus fünf und Sechs,
so sagt die Hex,
Mach Sieben und Acht,
so ist's vollbracht:
Und Neun ist Eins,
Und Zehn ist keins.
Tatsächlich geht zunächst alles auf, wenn man der Anleitung folgt und Zahlen in ein neunfeldriges Quadrat setzt:
Aus Eins mach Zehn: 10 kommt ins erste Feld; Zwei lass gehn, Drei mach gleich: 2 und 3 folgen; Verlier die Vier: Null; Aus Fünf und Sechs mach Sieben und Acht: schreibe erst 7 und 8, dann 5 und 6. Hat man's so weit getrieben, sieht das bis auf den letzten Platz gefüllte Quadrat so aus:
10 2 3
0 7 8
5 6
Die Quersummen in den fertigen Reihen und der Diagonale sind tatsächlich stets gleich, nämlich 15; um das gleiche Ergebnis aber auch für die letzte Reihe zu erreichen, darf man nun freilich nicht mehr der Hexen-Anleitung folgen (Und Neun ist Eins), sondern muss die verlorene Vier eintragen, was der ganzen Deutung einen nicht gerade klassischen Abschluss verleiht.
Man sollte eben, wie schon anfangs gesagt, nicht alles in Zahlen zu fassen versuchen, um es un-widerlegbar logisch zu beweisen. Da seien uns die Herren von der Insel Laputa eine eindringliche Warnung. Gulliver kam im Jahre 1707 auf seiner dritten Reise ins Reich der Mathematiker auf diese fliegende Insel, und er stellte von den Bewohnern fest: „Ihre Gedanken laufen bestän-dig in Linien und Figuren. Wenn sie zum Beispiel die Schönheit eines Weibes preisen wollten, beschrieben sie sie in Rhomben, Kreisen, Parallelogrammen, Ellipsen und anderen geometrischen Figuren.“ Kein Wunder, dass die Frauen da meuterten; und was war die Folge? Jonathan Swift beschrieb es: „Die Frauen der Insel sind von überroßer Lebhaftigkeit: sie verachten ihre Gatten und lieben die Fremden außerordentlich.“ Die konnten nämlich noch Komplimente machen, die nichts mit Zahlen und Linien zu tun hatten, sondern allenfalls mit Kurven. Und Frauen können bekanntlich selbst unumstößliche Axiome der Mathematik auf den Kopf stellen, wie etwa den Euklidschen Satz vom Ganzen, das mehr sei als sein Teil. Wieland hat das, den Blick aufs Dekolleté, sogar in einen Vers gefasst:
Wie man einen Blumenstrauß
Mit Vorteil an den Busen stecket,
Damit, durch eine kleine List
Die Hälfte, die er nicht bedecket,
Mehr als das Ganze ist .. .
Aber das gehört nun endgültig nicht mehr ins Reich der Zahlen und des Zählens.
Alles ist Zahl – zählen ist alles!
Herr Baedeker nahm es sehr genau; in seinen berühmten Reisehandbüchern musste alles stim-men. So bestieg er, um exakte Daten für seinen Italienband zu bekommen, auch den Mailänder Dom – um die Stufen zu zählen, die hinaufführen aufs Dach dieser berühmten, drittgrößten Kirche der christlichen Menschheit. Nun weiß jeder, der einmal abends im Bett Schäfchen gezählt hat, wie leicht man sich verzählt, sobald man in die höheren Zahlen gerät. Damit ihm ein solches Missgeschick nicht widerfahre – er hätte ja dem Dom ein zweites Mal aufs Dach steigen müssen – kam Herr Baedeker auf eine einfache, aber zweckmäßige Idee: Er steckte sich die Westentasche voller Trockenerbsen; sooft er nun zwanzig Stufen bewältigt hatte, entnahm er der Weste eine solche Hülsenfrucht und verlagerte sie in die Hosentasche. Oben angelangt, musste der Reisebuchautor nur noch die Erbsen in der Hosentasche zählen, mit 20 multiplizieren, den letzten Rest unter 20 hinzuzählen, und er hatte das Ergebnis.
Heutigentages wird sich kaum jemand die Mühe machen, Baedekers Zählwerk auf Genauigkeit zu prüfen, denn es führt inzwischen ein Aufzug hinauf aufs Domdach, zu der phantastischen Parade von 2245 Statuen und der vergoldeten Madonnina, dem Wahrzeichen Mailands.
Übrigens hätte Karl Baedeker es leichter haben können; zu seiner Zeit – er gründete den Reisebuchverlag 1827 – kannte man längst mechanische Zähler, ja, man hatte eigens Apparate konstruiert, um die Schritte eines Menschen zu zählen. Offenbar war es dem Menschen schon früh ein Bedürfnis, exakt feststellen zu können, ob und wann er zu weit gegangen sei, denn schon die alten Griechen kannten Wegmesser. Levinus Hulsius beschrieb in seinem 1615 in Frankfurt er-schienenen „Tractat von Mechanischen Instrumenten“ Bau und Funktion eines solchen Pedo-meters. Wie diese Dinger aussahen, kann man nachlesen im „Großen vollständigen Universallexikon aller Wissenschaften und Künste, welche bisher durch menschlichen Verstand und Witz erfunden und verbessert worden“, welchselbiges verlegt wurde von Johann Heinrich Zedier zu Leipzig und Halle Anno Domini 1749, dem Jahr, als Bach seine „Kunst der Fuge“ komponierte, als Mirabeau und Goethe geboren wurden. Dort heißt es unter dem Stichwort Schrittmesser: „Ein Instrument mit Rädern in einem Gehäus, auf die Art eines Uhrwercks, welches an den Gürtel der Beinkleider gehänget, und eine davon abgehende Schnur, so an einem aus dem Gehäus hervor-ragenden stühlenen Ärmlein angebunden, unten am Knie fest gemachet wird, welchergestalt bey einer jeden Spannung des Knies, die im Fortgehen geschiehet, das Ärmlein gezucket und durch dasselbe eines der inwendig verborgenen Rädlein fortgerücket, auswendig aber an denen mit Ziffern bezeichneten Scheiben durch gewisse Zeiger angewiesen wird, wie viel Schritte gethan worden. Das Instrument wird auf mehrerlei Weise zugerichtet.“ Hätte Baedeker die Technik so gut gekannt wie die Touristik, hätte er sich vermutlich einen solchen Compte-Pas ans Knie gebunden oder seinen Spazierstock damit bewaffnet, um der Qual der Zahl buchstäblich zu ent-gehen. Doch vielleicht war es gut, dass Baedeker an Fingern und Früchten des Feldes zählen musste, sonst wären seine Bücher am Ende gar voll von den Schrittzahlen, die eine Sehenswürdigkeit von der anderen trennen.
Immerhin, Baedeker hatte das Fehlen eines mechanischen Zählers auf schlaue Weise wettge-macht. Man muss allerdings feststellen, dass der Erbszähler zwar eine originelle, aber der Art nach keineswegs eine originale Erfindung dieses Herrn war; ja, man muss sogar einräumen, dass es anscheinend nicht einmal besonderer Intelligenz bedarf, um eine solche Zählhilfe zu erfinden und sich ihrer zu bedienen. Vielleicht schaffte das schon unser Ahn aus dem Neandertal, der ja bekanntlich noch nicht einmal die Ehre hatte, ein homo sapiens zu sein. Man kann diese Behauptung mit Beobachtungen aus neuerer Zeit untermauern, denn auf dieser Erde lebten vor kurzer Zeit Menschen noch auf der Stufe unserer Steinzeitler. Zum Beispiel: Auf Ceylon hausen noch ein paar hundert Weddas, Ureinwohner dieser Palmeninsel im Indischen Ozean. Inzwischen haben die meisten von ihnen eine richtige Sprache gelernt, nämlich die der Singhalesen, die in vorchristlicher Zeit aus Indien auf die Insel gekommen waren. Aber einige von ihnen, die Wald-Weddas, sind über das Tierefangen kaum hinausgekommen. Sie sind fast ausgestorben, obwohl sie keinen Herzinfarkt kennen, keine Bürostunden, keine Steuern; sie kennen aber auch keine Zahlen. In ihrer Ursprache gibt es einfach keine Wörter für zwei, drei, geschweige denn für mehr. Sie können überhaupt nicht zählen, blieben also auf einem geistigen Stand, den wir Zahlenmenschen heute nicht mehr verstehen, und den wir deshalb schlicht als primitiv bezeichnen.
Nun kommt aber auch der Wedda bisweilen in die Verlegenheit, etwas nach seiner Anzahl kon-trollieren zu müssen, und sei es nur, dass er feststellen will, ob ihm jemand eine Kokosnuss gemopst hat. Er muss also wissen, wie viele Nüsse er auf Vorrat hat. Wie aber schafft er das, wo er doch nicht zählen kann? Nun, er hat immerhin ein menschliches Gehirn, ist dem ebenfalls Nüsse sammelnden Eichhörnchen im Denken also überlegen; und er hilft sich ähnlich, wie es Baedeker tat: Der Wald-Wedda schnitzt sich eine Menge Stäbchen. Wenn er nun seinen Vorrat zählt, legt er für jede Kokosnuss ein Stäbchen beiseite und spricht dazu: „Das ist eins.“ Natürlich sagt er das auf Weddisch, aber das ist nahezu unbeschreiblich; Schrift kennen die Weddas nämlich auch nicht. Die Stäbchen verwahrt er getrennt von seinen Nüssen, damit ihm niemand listig mit einer Nuss zugleich ein Stäbchen entwende, um die Kontrolle zu erschweren. Man sieht: Auch Steinzeitmenschen kannten schon die berühmte soziologische Verhaltensregel „Trau, schau wem.“ Fragt man den Nüssesammler nun, wieviel Kokosfrüchte er habe, so sagt er nicht etwa „hundertzwanzig“, denn das kann er ja nicht; er zeigt vielmehr seine Stäbchen her und sagt: „Soviel.“ Gefühls- und erfahrungsgemäß weiß er, ob's ihm reichen wird oder nicht, ähnlich, wie ein Hausvater heute ja auch nicht die genaue Zahl der Eiform-Briketts in seinem Keller kennen muss, um zu wissen, ob er damit über den Winter kommt.
Mathematiker nennen Baedekers Erbsen oder die Stäbchen des Wedda eine Hilfsmenge, und Mathematik-Historiker würden den Erbszähler auf eine höhere Stufe stellen als den Stäbchenzähler, denn Baedeker hat für je 20 gezählte Stufen nur ein Stück seiner Hilfsmenge benützt, er hat sich der Zwanziger-Bündelung bedient. Derartige Zählhilfen gibt's in Hülle und Fülle, und jeder Mensch greift gelegentlich darauf zurück. Hätte jemand Albert Einstein gefragt, der wievielte Buchstabe im Alphabet das i sei, der große Physiker hätte wie jeder Stallknecht das ABC an den Fingern heruntergezählt, um zu der einfachen Zahl 9 zu gelangen, nur wäre er sich vermutlich bewusst gewesen, eine Hilfsmenge benützt zu haben. Einer Hilfsmenge bedient sich, bewusst oder unbewusst, auch der Ganove, der die Zahl seiner Hafttage in die Zellenwand ritzt und sich so einen ähnlichen Kalender herstellt, wie es weiland der baumschnitzende Robinson auf seiner einsamen Insel getan hat, oder wie es vor zweieinhalbtausend Jahren schon die alten Etrusker gemacht haben. Sie, so berichtet der römische Geschichtsschreiber Livius, hätten ein Gesetz gehabt, wonach „der oberste Prätor an den Iden des September (das war der 13.9. und zugleich Jahresanfang bei den Etruskern) einen Nagel einschlagen soll an der rechten Seite des Jupitertempels, wo das Heiligtum der Minerva liegt; man erzählt, dieser Nagel sei ein Zeichen für die Zahl der Jahre gewesen, weil damals Buchstaben und Zahlzeichen noch selten waren; weil die Zahl eine Erfindung der Minerva sei (sie war Beschützerin des Handwerks), war dies Gesetz in ihrem Tempel geweiht.“ Livius berichtet weiter, dass „auch in Bolsena solche Nägel im Tempel der etruskischen Göttin Nortia als Jahrzähler eingeschlagen wurden.“ Ein Taschenkalender war das ja gerade nicht, und man versteht, warum noch die Römer einen Computator brauchten, einen gelehrten Mann, dessen Hauptaufgabe die Berechnung der Zeit war, vor allem die Berechnung der Tage, auf die das Osterfest fiel. Dass sich davon unser Computer ableitet, sei nur so nebenbei erwähnt.
Ihnen allen, den Etruskern wie Robinson und dem Ceylon-Urwäldler, ging es darum, Gezähltes sichtbar und vor allem irgendwie dauerhaft zu machen. Man kann ja, will man sich die Zahl seiner erschlagenen Feinde merken, nicht zeitlebens mit fünf oder acht ausgestreckten Fingern herumlaufen, zumal man dann im Leben nichts anderes mehr zählen könnte und man die Finger ja hin und wieder auch zu etwas anderem braucht. Also band der Indianer sich die Skalpe um die Hüfte, der Kopfjäger hängte sich die Schrumpfköpfe vor die Tür als ermunterndes Willkommenszeichen, der afrikanische Neger behängte sich mit den Zähnen fürchterlicher Tiere, die er besiegt hatte, der Fidschi-Insulaner kerbte sich die Zahl seiner Himmelsbeförderungen in die Keule, der Philippino schlug sie mit Silbernägeln in die Klinge seines Schwertes, und der Jagdflieger pinselte sich für jeden Abschuss einen Triumph-Strich auf den Rumpf seiner Me 109. Das alles hatte natürlich vor allem die Funktion von Orden; gleichzeitig aber handelte es sich – mathematisch gesehen – um Hilfsmengen. Trafen sich zwei Supermänner im Busch, so konnten sie an den Trophäen leicht abzählen, wer von ihnen der Größte war.
Man sieht, das Zählen kann eine recht anschauliche und bunte Sache sein; allerdings ist bei solchen Verfahren die Funktionsfähigkeit des Registrierens ziemlich begrenzt. Könnten etwa zwei Offset-Drucker in einem modernen Betrieb auf die gleiche Art feststellen, wer von ihnen der schnellere sei? Schwerlich. Man stelle sie sich vor, wie sie zwischen Maschine und Wand hin- und herflitzten, um die Zahl der bedruckten Bogen mittels Strichen zu notieren! Das wäre die reinste Stummfilm-Groteske. Ein industrielles Zeitalter braucht rationellere Zählverfahren, zumal eines, das sich Benjamin Franklins Behauptung „Zeit ist Geld“ zur treibenden Devise gemacht hat. Und – bei Minerva! – dieses unser Zeitalter liebt das Zählen, denn es schätzt den Rekord, die Zuwachsrate, die Prozente, die Leistung, den Leistungsvergleich – und vor all das haben die Götter das Zählen gesetzt. Unsere Zeit ist stolz auf Zahlen, denn nur mit ihnen lassen sich die Hundertstelsekunden des Rennfahrers ausdrücken, die Milliarden des Staatsetats, die Maße des Filmidols, die Erfolge des Unternehmens, der Intelligenzquotient und die Dicke der Brieftasche.
Und überall und immer wieder wird gezählt: Wie viele Menschen in wie vielen Fabriken wie viele Einzelteile in wie vielen Arbeitsgängen und Minuten zu wie vielen Automobilen zusammenbauen; wie viele dieser Automobile über welche Kreuzungen fahren, wie viele von ihnen Unfälle machen, wie viele schadhafte Bremsen haben, wie viele Leute Autos fahren, wie viele Leute von Autos überfahren werden – man könnte einen Bandwurmsatz beliebiger Länge daraus machen. Gezählt werden an Druckmaschinen die Zahl der bedruckten Bogen, an Lichtschranken und Drehkreuzen die Zahl von Passanten, an Pressen die Hübe, an Stanzen die Stückzahlen, an Gleitzeitzählern die Stunden und Minuten, an Rundstrickautomaten die Zahl der Umdrehungen. Man zählt die Häupter eines Volkes, ihre Berufe, ihre Einkommen, ihre Häuser, ihre Kinobesuche, ihre Eisenbahnreisen, ihren Schnapskonsum – wer einmal ein statistisches Jahrbuch etwas eingehender studiert hat, der weiß, dass sich fast alle Sachinformationen über eine Nation in nackte Zahlen fassen lassen, und er ist vielleicht geneigt, Pythagoras zuzustimmen, der vor zweieinhalbtausend Jahren ein ganzes Weltbild und ein philosophisches Schulsystem auf dem Satz aufbaute: „Alles ist Zahl.“
Zählen und Zahl ist jedoch nicht nur Abschluss eines Vorgangs, sondern viel öfters Basis und Ausgangspunkt einer Unternehmung. Man zählte beispielsweise vom Flugzeug aus die Tiere im Serengeti-Park, nicht um sich hinterher auf die faule Löwenhaut zu legen und sich an einer neuen Statistik zu erfreuen, sondern um Anhaltspunkte dafür zu gewinnen, was man zum Schutz und zur Erhaltung der bedrohten Tiere tun könne. Und eine Verkehrszählung hat beileibe nicht den Zweck, sich über die Vielzahl von Autos zu freuen oder zu ärgern und die Zahlen dann ad acta zu legen, sondern um Daten für die Verkehrsplanung zu erhalten. Stückzählung an Maschinen ist einerseits Abschluss eines Produktionsvorgangs, andererseits auch wieder Ausgangspunkt beispielsweise für die Lohnberechnung. Mit anderen Worten: Zählen hat meist nur eine Nebenfunktion, aber oft eine entscheidende. Man könnte fast sagen: Zählen ist die wichtigste Nebensache der Produktion – und nicht nur der Produktion, denn gezählt wird überall: Vom fingerzählenden ABC-Schützen bis zum spektakulären Count-Down, von der Inventur bis zur Bilanz, vom spielerischen Zählen („Eins, zwei, drei, vier, Eckstein“) bis zum sturen Zählen („Links, zwo, drei, vier“), vom Geldnachzählen bis zum Kilometerzählen, vom Wiegen und Messen bis zum Rechnen und Kontrollieren – alles ist Zählen.
Man würde in jeder Fabrik Kompanien von Menschen finden, die mit nichts als zählen beschäftigt wären, hätte man das Zählen nicht längst vereinfacht, mechanisiert. Ohne Mechanisierung und Automatisierung des Zählens – des reinen Zählvorgangs – wäre der ganze industrielle Fortschritt buchstäblich nicht über drei hinausgekommen, so unglaublich das manchem klingen mag. Dass es überhaupt unglaublich erscheinen kann, ist jedoch nur ein Zeichen dafür, wie weit das Zählen schon mechanisiert (und damit dem Auge und einer Gehirntätigkeit entzogen) ist. Es fällt schon überhaupt nicht mehr auf, dass bei den meisten Arbeitsgängen automatisch mitgezählt wird, ja, dass allein durch Zählen schon ganze Produktionsabläufe gesteuert werden. Denn das Zählen ist ja längst über das Stadium des einfachen Abzählens hinaus. Aber wer denkt schon, wenn er am Armaturenbrett den Kilometerstand seines Wagens abliest, daran, dass hier einfach nur gezählt wurde, nämlich Radumdrehungen? Und wenn der Autofahrer tankt, wenn er im Parkhaus durch die Lichtschranke fährt, wenn er mit den Reifen die Kontaktschwelle an der Ampel berührt, wenn sein Wagen beim TÜV auf der Bremsprüfanlage steht – immer wird gezählt, und nicht nur aus Freude an Zahlen (höchstens am Bezahlen). Das Zählen gibt die Durchflussmengen an Tankstellen an und übersetzt sie automatisch in den Endpreis, es reguliert die Stockwerksbelegung in Parkhäusern, die Schaltung von Ampeln. Und darüberhinaus kann Zählen vielerlei Funktionen haben: Es kann Mischungen dosieren, Zeitabläufe regeln, die Stellung eines Magnetbandes angeben, Maschinen ein- und ausschalten, chemische Lösungen analysieren, Telefongespräche registrieren. Und wenn dereinst vollautomatische Fabriken den Menschen zum ewigen Faulenzen verbannen, so werden die steuernden Elektronenrechner die nötigen Informationen in Zahlen erhalten, von elektronischen Zählern, die an allen nötigen Punkten den Produktionsablauf ununterbrochen buchstäblich abzählen und die Zahlen fortlaufend der Zentrale übermitteln, die entsprechend ihrer Vorprogrammierung danach handelt und Entscheidungen trifft. Alles ist Zahl – die Weltformel des Pythagoras kann für die Welt der Technik eine neue Auslegung haben: Zählen ist alles.
Solche Folgen hat sich jener Urahn, der zuerst auf die Idee zu zählen kam, nicht träumen lassen. Wie kam er überhaupt darauf? Wollte er wissen, wie viele Frauen er hatte, um vor dem Höhlen-nachbarn zu prahlen? Fiel es ihm eines Tages auf, dass er mehr Finger als Arme hatte? Interes-sierte ihn die Zahl der Fische, die er fing? Nun, die Forscher sind sich ziemlich einig, wie und warum das Zählen „erfunden“ wurde (und die Herren aus dem Neandertal können sich ja nicht mehr wehren!). Sie sind der Meinung, dass das Zählen überhaupt nicht erfunden, erdacht wurde, wie etwa das Rad oder der Pflug, sondern dass es der natürlichen Empfindung „Ich-Du“ gewissermaßen entsprungen ist. Die ersten fühlenden und denkenden Menschen haben also zunächst nicht gezählt, sondern vielmehr nur den Unterschied zwischen Ich und Du, zwischen eins und einem anderen empfunden. Sie registrierten – mathematisch gesehen – Eins und Zwei, wenn sie auch noch nicht zählen konnten, sondern nur den Unterschied zwischen einem und dem anderen wahrnahmen. Daraus entwickelten sich dann die Zählstufen eins und zwei, die lange Zeit eine unüberwindliche Schwelle blieben: Man konnte anfangs im wahrsten Sinne des Wortes nicht bis drei zählen. Das scheint uns, die wir mit Milliarden umspringen, schier unvorstellbar. Aber auf der Erde laufen ja heute noch Anschauungsobjekte dafür frei herum. In Australien, Brasilien, Neu-Guinea und in der Südsee lebten noch bis weit in unser Jahrhundert hinein Menschen, die nur Worte für „eins“ und „zwei“ hatten; alles andere war ihnen „viel“. Und kam schon mal ein gewitzter Insulaner auf die Idee oder in die Verlegenheit, mehr als zwei Dinge zu zählen, so hatte er doch kein Wort für drei, vier, fünf, und er musste sich mit umständlichen Konstruktionen helfen: Er zählte „eins, zwei, zwei-eins, zwei-zwei, zwei-zwei-eins, zwei-zwei-zwei, zwei-zwei-zwei-eins“ und so weiter, so lange er eben in der Lage war, sich diese Bandwurmzahlen zu merken. Fürwahr eine primitive Zählerei, aber immerhin ein Anfang.
Und eines Tages bemerkte ein heller Kopf unter unseren Urahnen, dass ihm an den Händen eine ideale Hilfsmenge gewachsen war: die Finger. Nun konnte man wenigstens schon mal bis vier zählen – der Daumen wurde nämlich anfangs nicht mitgerechnet. Und das war schließlich der Beginn der unendlichen Zählreihe. Ein kritischer Leser mag freilich einwenden, woher man denn wisse, dass der frühe homo sapiens nur bis vier zählte, wo er doch nicht schreiben konnte und auch keine Tonbänder hinterließ. Man schloss einfach aus Bekanntem auf Unbekanntes; man stellte beispielsweise fest, dass sich alle im Laufe langer Zeit überwundenen Zählschwellen noch lange in Bräuchen erhielten. Das war so mit der Vierer-Schwelle und mit der Zwanziger-Schwelle, auf die wir gleich noch kommen werden. Die Inder, denen wir immerhin das Dezimalsystem verdanken, haben in ihrer Mythologie nicht die Zehn, nicht die Sechs oder die Fünf zur heiligen Zahl, sondern die Acht, die zweimal vier Finger der Hände, ohne die Daumen! In den Hinduländern Burma, Siam, Kambodscha und Malaya waren 4, 8, 16 und 32 immer wiederkehrende Zahlen, die Könige hatten gewöhnlich vier Hauptminister, vier Hauptfrauen (die im Islam zulässige Höchstzahl), acht Obersatrapen, sechzehn Untersatrapen. Und erst 1957 entschloss man sich in Indien, das Währungssystem zu dezimalisieren; bis zur Umstellung war das indische Kleingeld auf dem Vierersystem aufgebaut: eine Rupie hatte 16 Annas, eine Anna 4 Paises. Die Vierer-Zählgrenze lässt sich auch in dem römischen Brauch nachweisen, den Kindern nur bis zum vierten einen Namen zu geben; danach wurden die Sprösslinge einfach durchnumeriert: Quintus, Sextus, Septimus und so weiter. Auch im römischen Kalender, der ja mit dem März begann, hatten anfangs nur die vier ersten Monate einen Namen: Martius, Aprilis, Maius,Junius. Vom fünften an wurden schlicht Ordnungszahlen zu Monatsnamen: Quintilis, Sextilis, September, October, November, December. Später wurde dann der fünfte Monat zu Ehren des Gajus Julius Caesar in Julius umbenannt. Caesars Adoptivsohn und Erbe Octavian, der spätere Augustus, gab dann für den Monat Sextilis einen neuen Namen ab. Also verdankt unser September seinen Namen dem Umstand, dass unsere Vorfahren nicht gleich merkten, dass der Daumen ebenso zur Hand gehört wie die vier Finger. Als sie das aber erst einmal festgestellt hatten, da war des Zählens bald kein Ende mehr; man konnte nun leicht bis fünf und, wenn man beide Hände nahm, bis zehn zählen. Und da man barfuß lief, lag es nahe, auch die Zehen zum Zählen zu benützen und kam auf zwanzig. Diese Zahl war nun wieder fürs einfache Volk lange eine Grenze, die sich bis heute erhalten hat. Der Franzose sagt beispielsweise statt Achtzig: Vier-Zwanziger, quatre-vingt(s). Im Irischen heißt Zwanzig „fiche“, 40 wird gebildet als „da fiche“ (zwei Zwanzig), 60 als „tri fiche“ und so weiter bis 180: „naoi fiche“. Will also ein Ire 150 Jahre zählen, so sagt er „deich mbliadma secht fichit“, also zehn Jahre sieben zwanzig. Übrigens hat auch der Franzose noch im 18. Jahrhundert nicht nur 80 und 90, sondern auch andere Zahlen mit „vingt“, also mit zwanzig umschrieben. In Moliöres „Bürger als Edelmann“ tritt in der vierten Szene des dritten Akts ein Gläubiger auf, zieht das Schuldbuch und liest dem Schuldner die geliehenen Summen vor, unter anderem auch 120 Louisdor: „six-vingts louis“ (sechs Zwanziger). Eine berühmte Pariser Polizeitruppe von 220 Mann wurde „Les Onze-vingts“ genannt, die elf Zwanziger. Im 13. Jahrhundert baute Ludwig IX. in Paris ein Heim und Krankenhaus für 300 Blinde; es heißt heute noch „Quinze-vingts“ (15 Zwanziger = 300). Danach wird ein Blinder volkstümlich „un quinze-vingt“ genannt, und mit „entrer aux quinze-vingts“ (ins Blindenheim eintreten) wird das Schlafengehen umschrieben.
Man findet die Zwanzigerstufe noch in anderen Sprachen, so auch bei den heute fast ausgestor-benen Ainu, dem Urvolk Japans. Der Brauch hat sich im einfachen Volk oft auch dann noch erhalten, wenn die offizielle Sprache längst eine andere Zählreihe vorschrieb. So gab eine sizilianische Bäuerin vor nicht langer Zeit ihr Alter mit „tre vote vinti cincu anni“ an; sie war also 75, nämlich „drei mal zwanzig fünf Jahre“ (3 x 25). Und in französischen Rechnungsbüchern noch aus dem 18. Jahrhundert findet man etwa die Zahl 120 so geschrieben: Vlx. Man hatte sogar die Schreibweise dem Sprachgebrauch angepasst!
An den Fingern lernte der Mensch also über zwei hinauszuzählen; er tut's heute noch, als Kleinkind, das an den ungelenken Fingerchen bosselt und mühsam „ein-wei-dei-vier“ hersagt. Viel einfacher haben's da die Kleinen bei einigen Naturvölkern; sie brauchen keine abstrakten Zahlworte auswendig zu lernen, sondern umschreiben die Zahlen einfach nach der Stellung der Finger. Bei den Dene-Dindje-lndianern zum Beispiel heißt das Wort für die Zahl 1 wörtlich übersetzt: „Das Ende ist umgebogen“, und zwar das Ende der Hand, der Kleinfinger. Sie fangen nämlich – wie übrigens auch die Japaner – beim Fingerzählen nicht wie wir mit der geschlossenen Faust an, sondern mit der offenen Hand und beugen nacheinander einzelne Finger, wobei sie mit dem kleinen Finger beginnen. Entsprechend heißt das Wort für zwei: „Es ist nochmals umgebeugt“, und zwar diesmal der Ringfinger. Drei heißt dann „Die Mitte ist gebeugt“, vier: „Es ist einer übrig“, fünf: „An meiner Hand ist es fertig“. Da die Finger beim Zählen wie welkende Pflanzen abknicken, heißt das Wort für fünf in manchen Sprachen auch „Meine Hand stirbt“, für zehn „Meine Hände sind tot“, für fünfzehn: „Meine Hände sind tot und ein Fuß ist tot“ und für zwanzig: „Ein Mensch stirbt“ oder auch abgekürzt „Ein Mensch“. Da kommen natürlich beim Zählen lustige, aber auch recht umständliche Formulierungen heraus. Wollte etwa ein Missionar einem Papuastamm die Stelle aus Johannes 5, Vers 5 vorlesen: „Es war daselbst ein Mann 38 Jahre krank gelegen“, müsste er sich ungefähr so ausdrücken: „Ein Mann krank gelegen ein Mensch, beide Hände, ein Fuß und die Mitte ist gebeugt Jahre.“ Man stelle sich nun vor, wie es klänge, wenn ein Papuamädchen einem Mann ihre Telefonnummer zuflüsterte, oder wie ein Papuamann einem andern die Maße von Brigitte Bardot erklärt: „Ein Mensch und ein Mensch und ein Mensch und ein Mensch und beide Hände“, und damit hätte er erst die Oberweite erfasst.
Als der Mensch endlich über drei hinaus zählen konnte, war es für ihn bald ein Leichtes, in noch höhere Zahlenregionen vorzudringen, bis hundert und tausend zu zählen. Das Tausend war dann schließlich die letzte natürliche Zählschwelle, die lange nicht überwunden wurde. Alle Bezeichnungen für höhere Zahlen (Million, Milliarde, Billion und so weiter) sind nicht mehr quasi im Volk gewachsene, natürliche Wörter, sondern Kunstwörter, termini technici, eigens dafür erfunden, eine hohe Zahl auszudrücken. Man kam erst verhältnismäßig spät darauf. Noch Adam Riese, der berühmte Rechenmeister, der 1559 starb, nannte die Milliardenzahl 86 789 325178 umständlich so: „Sechs und achtzig tausent tausent mal tausent, siben hundert tausent mal tausent, neun und achtzig tausent mal tausent, drey hunderttausent, fünff und zwantzig tausent ein hundert acht und sibentzig.“ Er umschrieb also die Milliarde als „tausent tausent mal tausent“, die Million als „tausent mal tausent“, und er musste in diesen Tausendfüßler zur besseren Orientierung etliche Trennstriche einfügen. Wen wundert's da, dass das „Numerieren“, wie man damals das Lesen und Schreiben einer Zahl nannte, noch im Mittelalter eine Kunst für sich war.
